Řešení: a) a = 0
pCl = 1,00
b) a < 1
Vliv disociace je zanedbatelný, lze využít vztahu
(17)
[Cl–] = cCl – cAg =
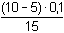 = 3,33·10–2 mol·l-1 = 3,33·10–2 mol·l-1
pCl = 1,48 Přídavek 9,99 ml 0,1M-AgNO3: nutno použít (16) [Cl–]r = cCl – cAg =
I = 0,05 pKs,c = 9,75 – 0,18 = 9,57
Ks,c = 2,69·10–10
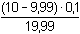 = 5·10–5
mol·l-1 = 5·10–5
mol·l-1pCl = - log
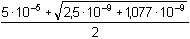 = 4,26 = 4,26Tento bod lze řešit také přičtením podílu [Cl–] z disociace sraženiny k neztitrovanému množství chloridů: [Cl–] = [Cl–]NaCl + [Cl–]AgCl =
[Cl–]r + [Cl–]s
Protože [Ag+]s = [Cl–]s, pak
Ks,c = [Cl–]s (5·10–5 +
[Cl–]s) = 2,69·10–10
Řešením kvadratické rovnice se obdrží
[Cl–]s = 4,90·10–6 mol·l-1
[Cl–] = 5·10–5 + 4,9·10–6 =
5,49·10–5 mol·l-1
pCl = 4,26
c) a = 1
Podle vztahu
(18):
pCl = 9,57/2 = 4,78
d) a > 1
[Ag+]r = cAg – cCl =
Podle
(19a):
pAg = 4,26 pCl = 5,31
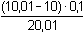 = 5·10–5
mol·l-1 = 5·10–5
mol·l-1Řešení lze provést také úvahou podobnou jako v případě b), neboť
[Ag+] = [Ag+]r + [Ag+]s =
5·10-5 + [Ag+]sPřídavek 12 ml 0,1 M-AgNO3: vliv disociace sraženiny je zanedbatelný, lze použít (19b): pAg = – log
I = 0,054 pKs,c = 9,56
pCl = 7,52
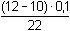 = – log 9,09·10–3
= 2,04 = – log 9,09·10–3
= 2,04 | ||