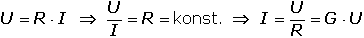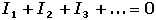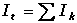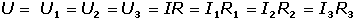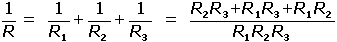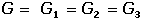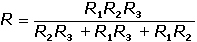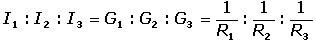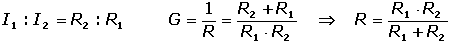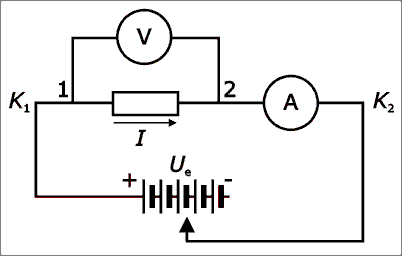
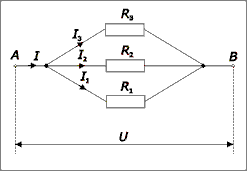
Jednoduchý elektrický obvod - Ohmův zákon

Připojením zdroje napětí U_e k lineárnímu rezistoru bude mezi body K₁ a K₂ protékat proud I. Bude-li elektrický odpor R rezistoru (vodiče), resp. vodivost G konstantní a vkládané napětí U proměnlivé, elektrický proud I bude úměrný vloženému napětí:

     (II.1)

Vztahy charakterizují vlastnosti lineárních vodičů, mají obecnou platnost a formulují se jako Ohmův zákon.

Elektrický odpor vodiče (rezistoru) se určí jako poměr napětí (mezi konci vodiče – body 1 a 2) a proudu, který jím protéká. Veličina U = R·I pak udává úbytek (pokles) napětí na rezistoru, jehož odpor je R.

II.1. Spojování rezistorů (odporů)

V rozvětvených obvodech (elektrických sítích) vztahy mezi elektrickými veličinami (napětí, proud, odpor, vodivost, kapacita) vyjadřují Kirchhoffovy zákony. Bod, ve kterém se rozvětvují tři nebo více vodičů se nazývá uzel, vodivá spojení mezi dvěma uzly jsou větve obvodu.

Rezistory spojené paralelně (vedle sebe)

1. Kirchhoffův zákon – algebraický součet proudů v uzlu se rovná nule

     (II.2)

(Pozn.: proudy vystupující z uzlu se označují znaménkem +, proudy vstupující do uzlu znaménkem –)

Vyjádřeno jinak – algebraický součet proudů tekoucích do uzlu sítě je roven součtu proudů z něho vystupujících:

     (II.3)

Napětí na rezistorech jsou stejná a rovnají se výslednému napětí: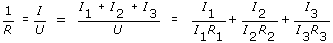

     (II.4)

     (II.5)

     (II.6)

Celkový odpor R tří paralelních větví bude:

     (II.7)

Proud se rozdělí do paralelních větví v poměru vodivostí:

     (II.8)

V případě dvou paralelních větví se proud rozdělí v obráceném poměru odporů:

     (II.9)

Souhrn:

Výsledný proud, resp. vodivost se rovná součtu dílčích proudů, resp. vodivostí.

Proudy ve větvích jsou úměrné vodivostem. Napětí na jednotlivých vodičích (rezistorech) je stejné.

Pozn.:

Paralelním připojením bočníku (shunt – viz kap. III.), je umožněno měření proudů větších než dovoluje rozsah měřiče proudu (ampérmetru).