|
- Příklad 4.21
- Vzorek cukru hmotnosti 0,4598 g byl rozpuštěn ve vodě a doplněn na objem 100 ml. Z tohoto
základního roztoku bylo odpipetováno 10 ml k voltametrickému stanovení kadmia a proudový
signál měl hodnotu 5,05 nA. Metodou regresní kalibrační křivky zjistěte koeficienty
a,b, jejich interval spolehlivosti
L(a,b)1,2 pro α = 0,05,
korelační koeficient r a procentový obsah kadmia v cukru. Kalibrační graf byl zkonstruován
z následujících dvojic dat: xi (ng/ml) - yi (nA):
0,562 - 0,38; 1,124 - 0,88; 1,168 - 1,50; 2,248 - 2,12; 2,81 - 2,63; 3,372 - 3,12;
3,934 - 3,62; 5,058 - 4,25; 6,182 - 5,38; 7,306 - 6,37; 8,43 - 7,13; 9,55 - 8,39.
Řešení:
Výsledky sestavíme do tabulky:
| n | xi [ng/ml] | yi [nA] | xi2 | yi2 | xi·yi
| | 1 | 0,562 | 0,38 | 0,3158 | 0,1444 | 0,2136
| | 2 | 1,124 | 0,88 | 1,2634 | 0,7744 | 0,9891
| | 3 | 1,168 | 1,50 | 1,3642 | 2,2500 | 1,7520
| | 4 | 2,248 | 2,12 | 5,0535 | 4,4944 | 4,7658
| | 5 | 2,810 | 2,63 | 7,8961 | 6,9169 | 7,3903
| | 6 | 3,372 | 3,12 | 11,3704 | 9,7344 | 10,5206
| | 7 | 3,934 | 3,62 | 15,4764 | 13,1044 | 14,2411
| | 8 | 5,058 | 4,25 | 25,5834 | 18,0625 | 21,4965
| | 9 | 6,182 | 5,38 | 38,2171 | 28,9444 | 33,2592
| | 10 | 7,306 | 6,37 | 53,3776 | 40,5769 | 46,5392
| | 11 | 8,430 | 7,13 | 71,0649 | 50,8369 | 60,1059
| | 12 | 9,550 | 8,39 | 91,2025 | 70,3921 | 80,1245
| | ∑ | 51,744 | 45,77 | 322,1853 | 246,2317 | 281,3978
|
(∑xi)2 = 2677,442 (∑yi)2 = 2094,8929
Výpočet koeficientů regresní rovnice podle
(21) a
(20):
b = 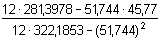 = 0,8483 nA·ml·ng-1 = 0,8483 nA·ml·ng-1
a = 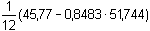 = 0,1563 nA
Závislost mezi proměnnými lze vyjádřit regresní rovnicí Yi = 0,1563 + 0,8483
· xi, která umožňuje výpočet směrodatných odchylek sy,x, sa
a sb podle
(22),
(23) a
(24),
případně nalézt odlehlý bod
(27):
| i | Yi | yi - Yi | (yi - Yi)2 | | i | Yi | yi - Yi | (yi - Yi)2
| | 1 | 0,6330 | -0,2530 | 0,0640 | | 7 | 3,4935 | 0,1265 | 0,0160
| | 2 | 1,1098 | -0,2298 | 0,0528 | | 8 | 4,4470 | -0,1970 | 0,0388
| | 3 | 1,1471 | 0,3529 | 0,1245 | | 9 | 5,4005 | -0,0205 | 0,0004
| | 4 | 2,0633 | 0,0567 | 0,0032 | | 10 | 6,3540 | 0,0160 | 0,0002
| | 5 | 2,5400 | 0,0900 | 0,0081 | | 11 | 7,3075 | -0,1775 | 0,0315
| | 6 | 3,0168 | 0,1032 | 0,0106 | | 12 | 8,2576 | 0,1324 | 0,0175
|
∑(yi - Yi)2 = 0,3676
s y,x = 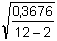 = 0,1917 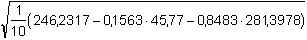 = 0,1918 = 0,1918
Vypočtené hodnoty Yi a naměřené yi se dobře shodují, pouze 3. bod se jeví
jako odlehlý. Test provedeme podle
(27)
T3 = 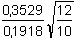 = 2,016 <
Tα = 2,387 pro (n-1) a α = 0,05 = 2,016 <
Tα = 2,387 pro (n-1) a α = 0,05
Bod regresní přímky není zatížen hrubou chybou.
pokračování řešení...
Zpět
|
|
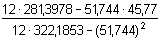 = 0,8483 nA·ml·ng-1
= 0,8483 nA·ml·ng-1
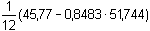 = 0,1563 nA
= 0,1563 nA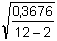 = 0,1917
= 0,1917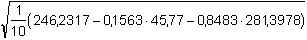 = 0,1918
= 0,1918
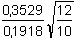 = 2,016 <
Tα = 2,387 pro (n-1) a α = 0,05
= 2,016 <
Tα = 2,387 pro (n-1) a α = 0,05