Pokračování řešení: Výpočet směrodatných odchylek regresních koeficientů podle (23) a (24):
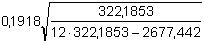 = 0,0998 = 0,0998
sb =
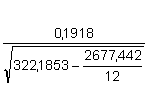 = 0,0193 = 0,0193Interval spolehlivosti koeficientů (25), (26):
L(b)1,2 = 0,8483 ± 0,0193·2,228 = 0,8483 ± 0,0430 nA·ml·ng-1
Hodnotu úseku otestujeme podle (28):
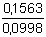 = 1,5661 < tα = 2,228 = 1,5661 < tα = 2,228
Parametr a se významně neliší od nuly a lze tedy jako kalibrační graf použít zjednodušenou
regresní rovnici
(29)
Yi = k·xi,
kde k = 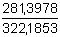 = 0,8734 nA·ml·ng-1
Yi = 0,8734·xi = 0,8734 nA·ml·ng-1
Yi = 0,8734·xi
Korelační koeficient r vypočítáme podle (31)
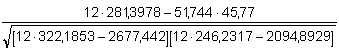 = 0,9974 = 0,9974
Hodnota r je blízká jedničce, tzn. že experimentální body prakticky leží na kalibrační přímce. Výpočet obsahu kadmia v analyzovaném vzorku:
a) Lze použít regresní rovnice (19) ve tvaru: 5,05 = 0,1563 + 0,8483·x
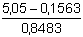 = 5,7688 ≈ 5,77 ng Cd/ml .....
5,13·10-8 mol·l-1 = 5,7688 ≈ 5,77 ng Cd/ml .....
5,13·10-8 mol·l-1
V původním objemu 100 ml je 10x více, tj. 57,7 ng Cd.
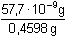 = 1,25·10-7 .....
1,25·10-5 % Cd = 1,25·10-7 .....
1,25·10-5 % Cd
x =
w = 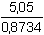 = 5,7820 ng Cd/ml .....
5,14·10-8 mol·l-1 = 5,7820 ng Cd/ml .....
5,14·10-8 mol·l-1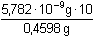 = 1,258·10-7 .....
1,26·10-5 % Cd = 1,258·10-7 .....
1,26·10-5 % Cd
V analyzovaném vzorku cukru je 1,26·10-5 % kadmia. | ||