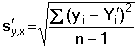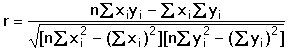| |||||
|
4.4. Lineární regrese kalibrační přímky Kalibrace je v analytické chemii nejběžnější vztah dvou proměnných veličin, kdy se zjišťuje závislost sledovaného signálu (závisle proměnná) na koncentraci analytu (nezávisle proměnná). Každá příčinná závislost dvou nebo více proměnných může v obecném pohledu vykazovat dvojí formu:
Regresní analýza lineární závislosti má za úkol určit odhady koeficientů a (posunutí) a b (směrnice), které charakterizují regresní přímku, vyjádřenou rovnicí Předpokládá se, že nezávisle proměnná x je prakticky bez chyby nebo aspoň s chybou podstatně menší než je chyba závisle proměnné y. Regresní analýza se uskutečňuje "metodou nejmenších čtverců", pro odhady regresních koeficientů platí následující vztahy (všechny ∑ pro i = 1 až n): Rozptyl hodnot závisle proměnných kolem regresní přímky (přesnost kalibrace) charakterizuje směrodatná odchylka sy,x kde Yi je hodnota vypočtená z regresní rovnice (19) pro odpovídající xi. Tato směrodatná odchylka sy,x umožňuje výpočet směrodatných odchylek koeficientů a, b rovnice: Interval spolehlivosti koeficientů rovnice se pak vypočítá podle vztahů Kritickou hodnotu tα pro počet stanovení (n – 1) a zvolenou hladinu významnosti nalezneme v tabulce 4. Body ležící výrazněji mimo regresní přímku (zatížené hrubou chybou) lze otestovat Grubbsovým testem: Je-li Ti > Tα (tab. 2) pro daný počet stanovení a hladinu významnosti, musí se výsledek vyloučit jako odlehlý a výpočet koeficientů regresní přímky se pak provede znovu. U přímkových kalibračních závislostí je koeficient a významnou veličinou - její nenulová hodnota svědčí o konstantní soustavné chybě; pokud je chyba kladná, lze ji eliminovat odečtením slepého pokusu, takže analytický signál by měl být nulový při x = 0. Zda je rozdíl regresního koeficientu a od nuly statisticky významný, se zjistí t-testem Hodnota t se porovnává s kritickou hodnotou tα Studentova rozdělení (tab. 4) pro počet stanovení (n – 1) a zvolenou pravděpodobnost. Pokud je t < tα, parametr a se významně neliší od nuly a mezi proměnnými lze předpokládat platnost jednoduchého funkčního vztahu kde směrnici k odhadujeme jako Těsnost rozložení závisle proměnné veličiny kolem lineární regresní přímky určuje korelační koeficient r Čím je hodnota korelačního koeficientu bližší ±1, tím je závislost mezi proměnnými těsnější a tím více se blíží přímce. Kladných hodnot nabývá pro přímou, záporných pro nepřímou závislost. Určení hodnoty koeficientu má praktický smysl až při větším počtu dvojic xi, yi. Někdy se setkáváme s případy nelineárních závislostí mezi proměnnými veličinami. O takovém případu se snadno přesvědčíme jednoduchou kontrolou. Pokud hodnoty poměru Δy/Δx náhodně kolísají kolem střední hodnoty, jedná se o lineární závislost. Vykazují-li pravidelnou změnu - vzestup či pokles - pak musíme předpokládat závislost nelineární. Matematické řešení nelineárních funkcí závisí na řadě podmínek podle typu závislosti. Nejčastější formou je transformace nelineární závislosti na lineární a pak se řeší výše popsanou metodou. Běžné postupy pro řešení nelineárních regresních závislostí lze nalézt v matematicko-statistické literatuře (např. Eckschlager K. a kol.: Vyhodnocování analytických výsledků a metod). Řešený příklad:
| ||
| |||||

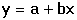
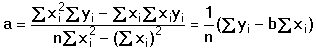
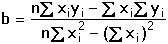
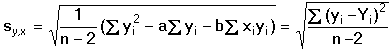
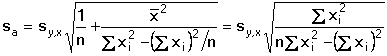
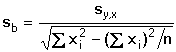
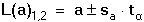
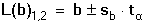
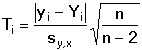
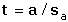
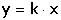
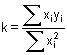 a směrodatná odchylka sy,x pak bude
a směrodatná odchylka sy,x pak bude