Řešení: Formální potenciály redoxních párů pro pH = 1 (podle vztahu (8b)):
 2 Cr3+ + 21 H2O 2 Cr3+ + 21 H2O
EfCr = 1,330 - 14
AsO43- + 2 e + 2 H3O+
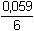 · 1 = 1,192 V
· 1 = 1,192 V AsO33- + 3 H2O AsO33- + 3 H2O
EfAs = 0,559 - 2
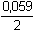 · 1 = 0,500 V
· 1 = 0,500 VTitrace probíhá podle rovnice
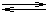 3 AsO43- + 2
Cr3+ + 12 H2O 3 AsO43- + 2
Cr3+ + 12 H2O
Látková množství reagujících složek:
nCr2O72- = 5 · 0,02 = 0,1 mmol
Protože platí: nAs = nCr2O72- · 3 =
nCr3+ · 3/2, vyplývá z toho, že obě složky systému zreagovaly
v ekvimolárních poměrech 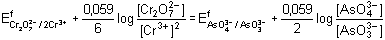 (E) (E)
Řešení A.: substituce složek ve zlomku na levé straně rovnice (E) redoxním párem AsO43-/AsO33-:
6 Eekv = 6 EfCr + 0,059 log
2 Eekv = 2 EfAs + 0,059 log
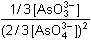 = 6 EfCr + 0,059 log = 6 EfCr + 0,059 log
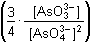 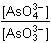
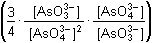 = == 6 EfCr + 2 EfAs + 0,059 log 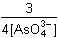
Eekv =
[AsO43-] = 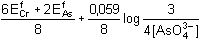 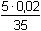 resp. resp.
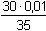 = 8,571·10-3
mol·l-1 = 8,571·10-3
mol·l-1
Eekv =
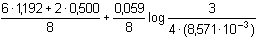 =
1,033 V =
1,033 VŘešení B.: substituce složek ve zlomku na pravé straně rovnice (E) redoxním párem Cr2O72-/Cr3+
6 Eekv = 6 EfCr + 0,059 log
2 Eekv = 2 EfAs + 0,059 log
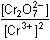 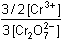 = 2 EfAs + 0,059 log = 2 EfAs + 0,059 log

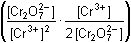 = 6 EfCr +
2 EfAs - 0,059 log (2 [Cr3+]) = 6 EfCr +
2 EfAs - 0,059 log (2 [Cr3+])
[Cr3+] =
Eekv = 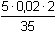 resp. resp.
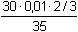 = 5,714·10-3
mol·l-1 = 5,714·10-3
mol·l-1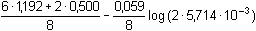 =
1,033 V =
1,033 V
| ||
 bod ekvivalence.
Platí rovnost potenciálů
bod ekvivalence.
Platí rovnost potenciálů