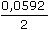Příklad VII.4.6 

Voltamogram dvouelektronové redukce kovového iontu M²⁺ v pufrovaném prostředí udává (E_1/2)_vol = -0,226 V (vs. SKE). Za nadbytku komplexotvorného ligandu (c_L = [L]) byly zaznamenány následující hodnoty (E_1/2)_k komplexu:

cL [mol/l]	0,02	0,04	0,06	0,08	0,10
(E1/2)k [V] (vs. SKE)	-0,494	-0,512	-0,523	-0,530	-0,536

Určete stechiometrický poměr složek komplexu a jeho konstantu stability.

Řešení

Výpočet hodnot ΔE_1/2 = (E_1/2)_vol – (E_1/2)_k pro dané koncentrace ligandu:

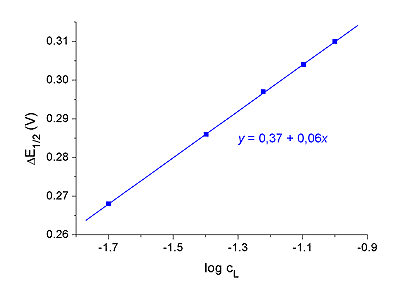
a) Řešení podle rovnice (VII.27): ΔE_1/2 = log β_p + p log c_L

0,268 = 0,0296 log β_p + p · 0,0296 log 0,02 | ·(-1)

0,310 = 0,0296 log β_p + p · 0,0296 log 0,10

0,042 = p (0,0503 – 0,0296) = p · 0,0203 p = 2,03 ≈ 2 ligandy

Výsledky p z dalších souborů rovnic: 2,03; 1,97; 2,07; 2,02; 2,02; 1,89; 2,04; 2,08; 2,02

Průměr 10 hodnot: p₁₀ = 2,02 ≈ 2 ligandy

Poměr centrálního kovového iontu a ligandu je 1:2 složení komplexu je ML₂

Konstanta stability β₂: 0,310 = 0,0296 log β₂ + 2 · 0,0296 log 0,10

log β₂ = 12,473 β₂ = 2,97·10¹²

Pozn.: Použije-li se p = 2,03, vyjde log β₂ = 12,503 a β₂ = 3,18·10¹²

b) Řešení pomocí regresní přímky pro funkci: ΔE_1/2 = f (log c_L)

ΔE_1/2 = log β_p + p log c_L

Graf závislosti ΔE_1/2 = f(log c_L):

Rovnice regresní přímky má tvar y = 0,37 + 0,06 x

ΔE_1/2 = 0,37 + 0,06 log c_L

Ze směrnice regresní přímky lze vypočítat počet ligandů p v komplexu:

0,06 = p p = 2,03 ≈ 2 ligandy

Úsek regresní přímky umožňuje vypočet konstanty stability β₂:

0,37 = 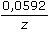log β₂ log β₂ = 12,5 a β₂ = 3,16·10¹²

Zpět