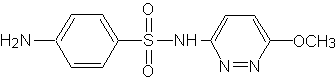|
VII.4. Využití polarografické/voltametrické křivky
Budou-li v elektrolyzovaném systému obě formy redoxního páru (např. Fe3+ a
Fe2+) a budou-li také elektrochemicky aktivní, vzniknou při polarizaci elektrody dva difúzní
proudy – katodický, odpovídající redukci oxidované formy, a anodický, odpovídající oxidaci redukované formy
v systému. Potenciál indikační elektrody, vyjádřený Petersovou rovnicí, je pak určen koncentracemi obou
redoxních forem na povrchu elektrody. Dosadíme-li z Ilkovičovy rovnice
(VII.12)
za rovnovážné koncentrace, získáme po úpravě rovnici polarizační křivky jako funkční závislost
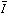 = f(E). = f(E).
Rovnice anodicko-katodické vlny (Heyrovského-Ilkovičova) pro reakci: Ox + ze
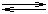 Red Red
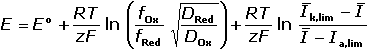 (VII.18) (VII.18)
První dva členy rovnice tvoří konstantu pro danou reakci – půlvlnový potenciál E1/2:
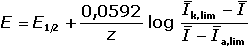 (pro 25 °C) (VII.19) (pro 25 °C) (VII.19)
Bude-li koncentrace formy Red v roztoku velmi malá (coRed ≈ 0;
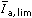 → 0), vznikne katodická
vlna a rovnice bude mít tvar: → 0), vznikne katodická
vlna a rovnice bude mít tvar:
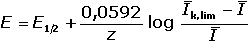 (pro 25 °C) (VII.20) (pro 25 °C) (VII.20)
Rovnic lze využít k určení počtu elektronů spotřebovaných při elektrodové reakci a k potvrzení reversibilty
systému. K tomuto účelu se používá tzv. "logaritmické analýzy polarografických křivek" – pro katodickou
redukci má rovnice tvar přímky:
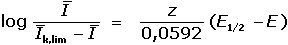 (VII.21) (VII.21)
Analogické vztahy lze odvodit pro reversibilní anodickou oxidaci.
Rovnice reversibilní anodicko-katodické vlny s účastí protonů: Ox + ze + mH+
 Red Red
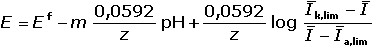 (VII.22) (VII.22)
První dva členy pravé strany rovnice tvoří pro danou reakci konstantu E1/2:
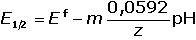 (pro 25 °C) (VII.23) (pro 25 °C) (VII.23)
Předpokládejme, že polarograficky aktivní kovový ion Mz+ tvoří komplex s ligandem L-:
Mz+ + pL–  MLp(p-z)–, s konstantou stability
MLp(p-z)–, s konstantou stability 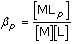 .
Komplexně vázaný kovový ion se redukuje za vzniku amalgámu: MLp + xHg +
ze → M(Hg)x + pL. .
Komplexně vázaný kovový ion se redukuje za vzniku amalgámu: MLp + xHg +
ze → M(Hg)x + pL.
Vztah pro polarografickou křivku redukce komplexu se odvodí z Petersovy rovnice, v níž se za koncentraci
Mz+-iontu na povrchu elektrody dosadí hodnoty konstanty stability
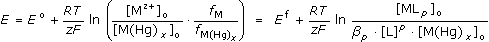
Po dosazení z Ilkovičovy rovnice (VII.12)
za koncentrace komplexu a amalgám kovu na povrchu elektrody se získá tvar rovnice pro potenciál
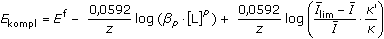
resp.
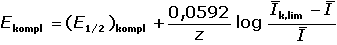 (pro 25 °C) (VII.24) (pro 25 °C) (VII.24)
Konstantu (E1/2)kompl tvoří první dva členy rovnice a poměr Ilkovičových konstant
κ a κ' pro komplex
a amalgám kovu:
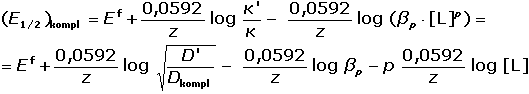 (VII.25) (VII.25)
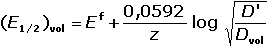 (VII.26) (VII.26)
Z rozdílu E1/2 volného a vázaného kovového iontu lze vypočítat
βp nebo počet ligandů p:
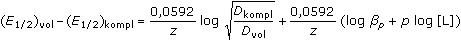
resp. za předpokladu, že Dvol ≈ Dkompl
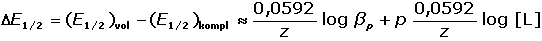 (VII.27) (VII.27)
Příklady
- Příklad VII.4.1




- Ze záznamu reversibilní katodické vlny byly odečteny hodnoty:
| Ek(SKE) [V] | –0,587 | –0,598 | –0,607 | –0,614 | –0,623
| 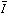 [μA] [μA] | 0,82 | 1,65 | 2,48 | 3,30 | 4,13
|
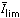 = 5,51 μA = 5,51 μA
Vypočítejte počet vyměněných elektronů při elektrodové reakci a Eo (proti SKE)
redoxního páru za předpokladu, že DOx = DRed a
fOx = fRed. ESKE = 0,241 V
- Příklad VII.4.2




- Reversibilní redukce nitrobenzenu v Britton-Robinsonových pufrech byla provedena na visící rtuťové
elektrodě metodou DPV s rychlým nárůstem polarizačního napětí (20 mV/s) a s modulační amplitudou
pravoúhlého pulsu –50 mV. Projevem redukce byly dva proudové píky, analyticky významný byl 4-elektronový
první pík. Pro vybrané hodnoty pH byly odečteny následující potenciály píku Ep1:
| pH | 2,07 | 3,62 | 4,78 | 6,68 | 9,44
| | Ep1 [V] (vs. Ag/AgCl/1M-KCl) | -0,117 | -0,208 | -0,274 | -0,391 | -0,557
|
Kolik protonů se účastnilo elektrodové reakce?
- Příklad VII.4.3




- Při redukci sulfamethoxypyridazinu (antibiotikum ze skupiny sulfonamidů) v prostředí minerální kyseliny
a tlumivých roztoků a za konstantní iontové síly analyzovaného roztoku byly odečteny hodnoty potenciálu
voltametrických píků:
| Ep [V] | -0,600 | -0,625 | -0,640 | -0,672 | -0,740 | -0,805 | -0,865 | -0,935
| | pH | 1,33 | 1,75 | 2,00 | 2,60 | 3,47 | 4,20 | 4,93 | 5,67
|
Elektrodová redukce probíhá na pyridazinovém jádře a je dvouelektronová, na volné aminoskupině probíhá
protolytická reakce (pKa ≈ 2,8). Zjistěte počet protonů zapojených do reakce při pH
< pKa a při pH > pKa a vytvořte schéma mechanismu redukce látky v kyselém
prostředí.
Strukturní vzorec sulfamethoxypyridazinu: 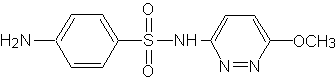
- Příklad VII.4.4




- Organická látka chinoidní struktury (2-aminofenoxaz-3-on) byla podrobena polarografické redukci
v závislosti na aciditě. Z křivek byly odečteny hodnoty E1/2 (vs. SKE)
= f(pH):
| pH | 1,0 | 1,5 | 2,5 | 4,0 | 4,5 | 6,0 | 7,0 | 8,0 | 11,0 | 12,0
| | E1/2 [V] | 0,159 | 0,129 | 0,049 | -0,087 | -0,133 | -0,238 | -0,301 | -0,359 | -0,511 | -0,540
|
Zjistěte počet protonů při dvouelektronové redukci látky v jednotlivých oblastech pH, vymezených
disociačními konstantami (pKox = 1,99; pKr1 = 4,95;
pKr2 = 10,10). Jaký bude E1/2 při pH = 0 (tj.
Ef)? Předpokládejte, že fox ≈ fred
a Dox ≈ Dred. Vytvořte obecně formulované schéma
mechanismu redukce látky.
Strukturní vzorec 2-aminofenoxaz-3-onu: 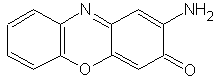
- Příklad VII.4.5




- Při redukci Cd2+-iontu vázaného komplexně s ethylendiaminem (en), byla z polarografických vln získána následující data:
| cen [mol/l] | 0,00 | 0,10 | 0,50 | 1,00 | 2,00
| | E1/2 [V] vs. SKE | –0,578 | –0,842 | –0,906 | –0,934 | –0,964
|
Vypočítejte počet ligandů v komplexu a konstantu stability, je-li z = 2. Aktivitní koeficienty
látek reagujících na elektrodě považujte za jednotkové, vliv difúzních koeficientů zanedbejte.
- Příklad VII.4.6




- Voltamogram dvouelektronové redukce kovového iontu M2+ v pufrovaném prostředí udává
(E1/2)vol = -0,226 V (vs. SKE). Za nadbytku komplexotvorného
ligandu (cL = [L]) byly zaznamenány následující hodnoty
(E1/2)k komplexu:
| cL [mol/l] | 0,02 | 0,04 | 0,06 | 0,08 | 0,10
| | (E1/2)k [V] (vs. SKE) | -0,494 | -0,512 | -0,523 | -0,530 | -0,536
|
Určete stechiometrický poměr složek komplexu a jeho konstantu stability.
|
|

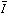 = f(E).
= f(E). Red
Red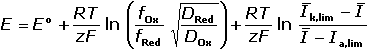
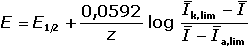
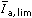
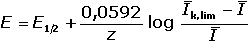
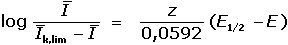
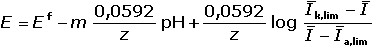
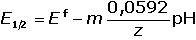
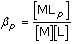 .
Komplexně vázaný kovový ion se redukuje za vzniku amalgámu: MLp + xHg +
ze
.
Komplexně vázaný kovový ion se redukuje za vzniku amalgámu: MLp + xHg +
ze 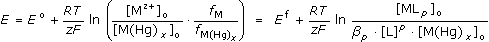
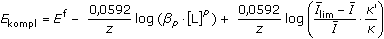
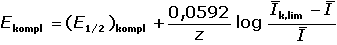
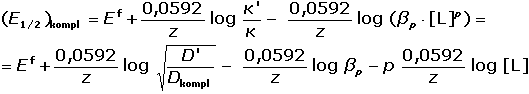
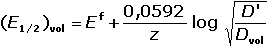
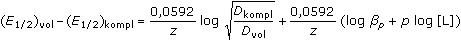
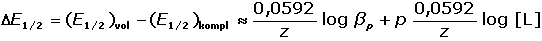




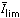 = 5,51 μA
= 5,51 μA