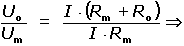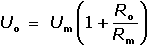|
III.4. Měření kapacity
Kapacita (kondenzátoru) je veličina charakterizující schopnost kondenzátoru jímat volný elektrický náboj.
Definována je vztahem
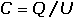 (III.12) (III.12)
kde U je elektrické napětí mezi kladnou a zápornou elektrodou kondenzátoru o náboji Q.
K měření kapacity jsou konstruovány specielní kapacitní můstky, v nichž jsou vestavěny normální kondenzátory
o známé kapacitě, které je možno dle libosti zařazovat a na stupnici pak odečítat hodnotu příslušné veličiny.
Lze však použít i běžný kompenzační Wheatstoneův můstek, používaný ke srovnávání odporů, napájený střídavým
napětím. Nahradíme-li v můstku rezistory R1 a R2 kondenzátory
C1 (= Cx) a C2, pak při vyvážení obvodu platí
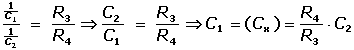 (III.13) (III.13)
III.5. Měření rovnovážného potenciálu článků
Pro běžné měření elektromotorického napětí (EMN) článků jsou vhodné výchylkové metody, avšak přesnější
jsou metody kompenzační. V současnosti se již používají digitální voltmetry, které udávají hodnotu
měřeného napětí odpovídajícím číslem na 3 až 7 platných míst podle typu přístroje. Protože vnitřní
odpor přístroje není nekonečný, prochází voltmetrem při měření proud, který může výrazně ovlivnit
měřené napětí i napětí zdroje. Přesné měření je tedy nezbytné provést tak, aby proud tekoucí voltmetrem
byl nulový nebo aspoň zanedbatelný. Toho lze dosáhnout použitím některé kompenzační metody nebo výchylkovou
metodou s voltmetrem, který má vysoký vstupní odpor.
a) Kompenzační (Poggendorfova) metoda
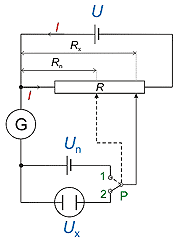
Princip spočívá v tom, že měřené napětí se porovnává se známým napětím odvětveným
z potenciometru, napájeného ze zdroje napětí U. Při rovnosti měřeného napětí Ux
s napětím odvětveném na potenciometru (I Rx) je na indikátoru G nulové napětí.
Pak Ux = U (Rx / R). Pro přesná měření
se potenciometr kalibruje pomocí Westonova článku (Un = 1,0183 V při 20 °C).
Pak platí
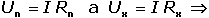 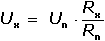 (III.14) (III.14)
b) Výchylková (přímá) metoda
 Správnost měřeného napětí článku je závislá na hodnotě vstupní impedance měřicího přístroje,
která musí být aspoň o 2-3 řády vyšší, než je odpor článku. Připojí-li se k článku, který má odpor
Ro měřidlo o vstupní impedancí Rm, poměr napětí článku
Uo a hodnoty na měřidle Um bude v poměru odporů podle vztahu
Správnost měřeného napětí článku je závislá na hodnotě vstupní impedance měřicího přístroje,
která musí být aspoň o 2-3 řády vyšší, než je odpor článku. Připojí-li se k článku, který má odpor
Ro měřidlo o vstupní impedancí Rm, poměr napětí článku
Uo a hodnoty na měřidle Um bude v poměru odporů podle vztahu
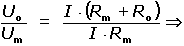 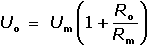 (III.15) (III.15)
Příklady
- Příklad III.5.1




- Potenciometr kompenzačního zařízení má celkový odpor 1000 Ω. Jaké rovnovážné napětí má galvanický
článek, jestliže při vynulování galvanometru byla odečtena hodnota 460 ohmů a po zařazení Westonova
článku 840 Ω?
- Příklad III.5.2




- Při měření napětí článku kompensační metodou bylo jako nulového indikačního přístroje použito
ručkového galvanometru o vnitřním odporu 40 Ω. Odpor měřeného článku činí 160 Ω.
Jaký proud protéká obvodem, je-li rozdíl mezi měřeným a srovnávacím napětím 20 mV?
- Příklad III.5.3




- Napětí článku je 200 mV. Obvodem protéká proud 5·10–7A. Jaká je chyba měření,
je-li vnitřní odpor článku a) 100 Ω, b) 10 kΩ?
- Příklad III.5.4




- Odpor skleněné elektrody je 500 MΩ při 25 °C, vstupní impedance pH-metru je
2·1011 Ω. Je vstupní impedance dostačující? Jaké chyby se dopustíme,
když naměřená hodnota je Um = 0,624 V ?
- Příklad III.5.5




- Odpor skleněné elektrody je 660 MΩ při 25 °C, vstupní impedance pH-metru je
3·1010 Ω. Jak velké chyby se dopustíme, jestliže naměříme napětí 0,841 V ?
|
|

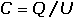
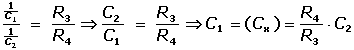

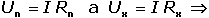
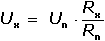
 Správnost měřeného napětí článku je závislá na hodnotě vstupní impedance měřicího přístroje,
která musí být aspoň o 2-3 řády vyšší, než je odpor článku. Připojí-li se k článku, který má odpor
Ro měřidlo o vstupní impedancí Rm, poměr napětí článku
Uo a hodnoty na měřidle Um bude v poměru odporů podle vztahu
Správnost měřeného napětí článku je závislá na hodnotě vstupní impedance měřicího přístroje,
která musí být aspoň o 2-3 řády vyšší, než je odpor článku. Připojí-li se k článku, který má odpor
Ro měřidlo o vstupní impedancí Rm, poměr napětí článku
Uo a hodnoty na měřidle Um bude v poměru odporů podle vztahu