| |||||
|
K analytickým výpočtům používáme údaje zjištěné s různou přesností. Výsledky jednotlivých měření je třeba udávat na tolik desetinných míst, aby pouze poslední bylo nejisté. Je tedy ustálenou zvyklostí uvádět ve výsledku o jedno desetinné místo více, než je počet míst se zaručenou přesností. Např. ze dvou paralelních stanovení dusíku v organické látce 18,29 % a 18,06 % lze jako výsledek použít 18,2 % - tedy jen tři platná čísla, protože v aritmetickém průměru (18,175 %) již třetí číslo nelze zaručit. Přesná hodnota velkého počtu používaných čísel vyjadřujících velikost různých veličin není známa. V takových případech se místo přesných hodnot používají hodnoty přibližné, které se dosazují do matematických vztahů. Výsledek je pak rovněž přibližným číslem, je tedy zatížen větší nebo menší chybou. Hodnoty se zbytečně velkým počtem desetinných míst, jejichž přesnost nelze zaručit, se zaokrouhlují. Zaokrouhlovat však smíme tehdy, jestliže zaokrouhlením vzniklá relativní chyba je zanedbatelně malá proti chybě stanovení. Hodnoty získané měřením zaokrouhlovat nelze - výpočet se provede s jejich plnou hodnotou a teprve konečný výsledek se zaokrouhlí. O způsobu zaokrouhlování rozhoduje číslice, která následuje za poslední číslicí, jež má být ponechána v čísle:
Kalkulačky, které operují s větším počtem desetinných míst, zaokrouhlují pětku vždy nahoru. Při jejich použití je třeba dbát, aby počet platných číslic nebyl větší, než má nejméně přesné číslo použité k výpočtu nebo než má změřený a k výpočtu použitý údaj. Kromě chyb zaokrouhlovacích se na úrovni výsledků analýz podílí další chyby, jejichž příčiny mnohdy ani nelze zjistit. Chyba je však ukazatelem nesouladu mezi výsledkem stanovení (měření) a skutečným obsahem (hodnotou měřené veličiny) sledované složky ve vzorku. Vyjadřuje se jako chyba absolutní nebo relativní. Absolutní (prostá) chyba di je algebraický rozdíl mezi nalezeným výsledkem xi a skutečnou hodnotou μ a může být kladnou nebo zápornou veličinou, ale vždy pojmenovanou. Může být mírou reprodukovatelnosti v sérii analýz. Relativní (poměrná) chyba ei je vztažena ke skutečné (správné) hodnotě, je tedy mírou správnosti. Je veličinou nepojmenovanou, obvykle uváděnou v procentech. Pokud ke skutečné hodnotě vztahujeme aritmetický průměr 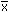 výsledků série měření
Relativní chyba je mírou přesnosti jednotlivých stanovení. výsledků série měření
Relativní chyba je mírou přesnosti jednotlivých stanovení.
Podle toho, jak se chyby ve výsledku projevují, může se jednat o chyby náhodné, soustavné a hrubé. Pokud v sérii měření vznikají pouze náhodné chyby (jednotlivé výsledky se vzájemně dobře shodují), výsledky jsou přesné a správné, jsou tedy spolehlivé. Přesné výsledky však nemusí být vždy současně správné, mohou se od správného výsledku lišit o hodnotu soustavné chyby. Příčinu této chyby je třeba odhalit a postup analýzy upravit tak, aby v opakovaném měření byly výsledky přesné a správné. Výsledky nepřesné jsou analyticky nepoužitelné. Ojedinělý výsledek, který se od ostatních významně liší, se označuje jako odlehlý, zatížený hrubou chybou. | ||
| |||||

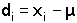
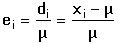
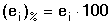 (2)
(2)