



Řešení
(Σyi)2 = 66,0969 Výpočet koeficientů regresní rovnice y = a + bx podle vztahů (21) a (20):
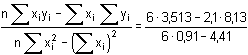 = 3,814 = 3,814a = 1/n (Σyi - b Σxi) = 1/6 · (8,13 - 3,814 · 2,1) = 0,020 Závislost mezi proměnnými vyjadřuje rovnice: Y = 0,020 + 3,814·x. Vypočtenými hodnotami Y doplníme tabulku. Z rozdílu naměřených (závisle proměnných) a vypočtených hodnot (y – Y) je zřejmé, že 4.bod leží výrazně mimo regresní přímku. Tento bod otestujeme Grubbsovým testem (kombinace vztahů (22) a (27)):
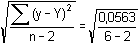 = 0,1186 = 0,1186Směrodatná odchylka sx,y charakterizuje rozptyl hodnot xi kolem regresní přímky.
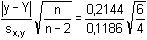 = 2,214 > Tα=0,05 = 1,996 = 2,214 > Tα=0,05 = 1,996Z Grubbsova testu je zřejmé, že bod 4 je třeba vyloučit a provést nový výpočet pouze s pěti dvojicemi proměnných.
(Σy)2 = 40,5769
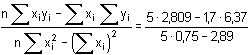 = 3,740 = 3,740a = 1/n (Σyi - b Σxi) = 1/5 · (6,37 - 3,740 · 1,7) = 0,0024 Výpočet směrodatných odchylek koeficientů a,b regresní rovnice pomocí vztahů (22), (23) a (24):
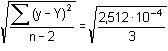 = 9,150·10-3 = 9,150·10-3sa = sx,y sb = 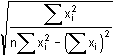 = 9,150·10-3 · = 9,150·10-3 · 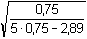 = 0,0085 = 0,0085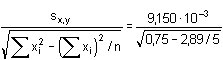 = 0,022 = 0,022
 = = 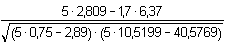 = 0,9999 = 0,9999 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||