|
- Příklad 4.24




- Ve vzorku bylo stanoveno železo fotometricky na základě měření absorbance komplexu
s kyselinou sulfosalicylovou v alkalickém prostředí. K analýze bylo naváženo 0,1241 g
vzorku, po převedení do roztoku byl objem doplněn na 250 ml. Z tohoto základního roztoku
bylo pipetováno po 0,50 ml do odměrných baněk objemu 25 ml. Po přídavku reakčních
komponent byl roztok doplněn a proměřován. Absorbance třech roztoků byla:
0,455, 0,452, 0,456. Hodnoty kalibračních roztoků jsou následující (μg Fe - A):
0,038 - 0,106; 0,154 - 0,235; 0,306 - 0,402; 0,381 - 0,495; 0,449 - 0,580; 0,762 - 0,920.
Zjistěte, zda kalibrační regresní přímka prochází počátkem os! Vypočtěte procentový obsah
železa ve vzorku!
Řešení | n | x
[μg Fe] | y
[A] | Y | y – Y | x2 | y2 | xy | 1
2
3
4
5
6 | 0,038
0,154
0,306
0,381
0,449
0,762 | 0,106
0,235
0,402
0,495
0,580
0,920 | 0,1056
0,2367
0,4085
0,4933
0,5701
0,9238 | 0,0004
-0,0017
-0,0065
0,0017
0,0099
-0,0038 | 0,0014
0,0237
0,0936
0,1452
0,2016
0,5806 | 0,0112
0,0552
0,1616
0,2450
0,3364
0,8464 | 0,0040
0,0362
0,1230
0,1886
0,2604
0,7010 | | Σ | 2,09 | 2,738 | | | 1,0461 | 1,6558 | 1,3132 |
(Σx)2 = 4,3681(Σy)2 = 7,4966 Výpočet koeficientů regresní rovnice y = a + bx podle vztahů (21) a (20): b = 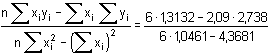 = 1,1301 = 1,1301a = 1/n (Σyi - b Σxi) = 1/6 · (2,738 - 1,1301 · 2,09) = 0,0627 Závislost mezi proměnnými vyjadřuje rovnice: Y = 0,0627 + 1,1301·x. Vypočtenými hodnotami Y doplníme tabulku. Z rozdílu naměřených (závisle proměnných) a vypočtených hodnot (y – Y) je zřejmé, že všechny body leží těsně kolem regresní přímky a lze ji tedy použít jako přímky kalibrační. Stanovení železa v analyzovaném vzorku: absorbance: 0,4550,452 0,456
průměr: 0,4543 Obsah železa se vypočítá z regresní rovnice 0,4543 = 0,0627 + 1,1301·x x = 0,3465 mg Fe v 0,50 ml vzorku Procentový obsah železa v objemu 250 ml:(w)Fe = 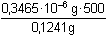 · 100 = 0,14 % · 100 = 0,14 % Zpět
|
|




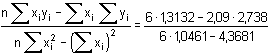 = 1,1301
= 1,1301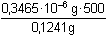 · 100 = 0,14 %
· 100 = 0,14 %