|
- Příklad 5.74




- Jaké pH bude mít směs 40 ml 0,05M-(NH4)2SO4 a 50 ml
0,1M-NaOH za předpokladu úplné disociace hydroxidu sodného. Výpočet s ohledem na iontovou
sílu roztoku proveďte přibližně i přesně!
Řešení Smícháno bylo:40 · 0,05 = 2 mmol (NH4)2SO4 = 4 mmol NH4+50 · 0,1 = 5 mmol NaOH Vzájemnou reakcí (NH4)2SO4 a NaOH vznikne NH4OH, přebytek NaOH bude určovat pOH (pH) a ionty Na+ a SO42- se budou podílet na iontové síle roztoku.Výsledná koncentrace OH–: [OH–] = 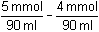 = 0,0111 mmol·ml–1 = mol·l–1 = 0,0111 mmol·ml–1 = mol·l–1 Iontová síla roztoku:I = 1/2(0,0111·12 + 0,0556·12 + 0,0222·22) = 0,0778OH– Na+ SO42- a) Aktivitní koeficient a aktivita OH–-iontu:– log fOH- = 0,509·1· = 0,1110 = 0,1110  fOH- = 0,7744 fOH- = 0,7744a OH- = 0,0111 · 0,7744 = 8,60·10 –3 mol·l –1  pOH = 2,06  ) – 2,06 = 13,78 – 2,06 = 11,72 ) – 2,06 = 13,78 – 2,06 = 11,72 b) Protože 0,05 cNaOH < [OH–] > 0,05 cNH4OH, lze předpokládat, že podíl disociace slabé zásady není zanedbatelný (řešení podle vztahu (44), upraveného pro [OH–].Z disociační rovnováhy NH3 + H2O 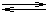 NH4+ + OH- vyplývá, že NH4+ + OH- vyplývá, že[NH4+]dis. = [OH–]dis. = x[NH3] = cNH3 - x = 4/90 - x = 0,0444 - x ≈ 0,0444 mmol·ml–1 = mol·l–1 Rovnováhu charakterizuje konstanta basicity ovlivněná iontovou sílou roztoku:pKB,c = 4,755 –  = 4,755 – 0,218 = 4,537 = 4,755 – 0,218 = 4,537K B,c = 10 –4,537 = 2,904·10 –5 = 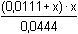 Podíl disociace vyplyne řešením kvadratické rovnice:x2 + 0,0111 x – 1,29·10–6 = 0x = [OH–]dis. = 1,12·10–4 mol·l–1 Celková koncentrace OH–-iontu a výsledná hodnota pH bude:[OH–] = 0,0111 + 1,12·10–4 = 0,011212 mol·l–1  pOH = 1,95 pOH = 1,95pH = pKw,c – pOH = 13,78 – 1,95 = 11,83 Zpět
|
|




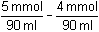 = 0,0111 mmol·ml–1 = mol·l–1
= 0,0111 mmol·ml–1 = mol·l–1 = 0,1110
= 0,1110  fOH- = 0,7744
fOH- = 0,7744 pOH = 2,06
pOH = 2,06 ) – 2,06 = 13,78 – 2,06 = 11,72
) – 2,06 = 13,78 – 2,06 = 11,72 NH4+ + OH- vyplývá, že
NH4+ + OH- vyplývá, že = 4,755 – 0,218 = 4,537
= 4,755 – 0,218 = 4,537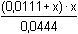
 pOH = 1,95
pOH = 1,95