



Řešenía) Podle Debye-Hückel-Onsagerovy rovnice (VIII.6) pro vodivost HNO3 platí Λ = Λo - (A + B · Λo) · kde číselné konstanty mají hodnotu (pro 25 °C) A = 60,65 a B = 0,230. Λo = λo(H+) + λo(NO3-) = 349,81 + 71,46 = 421,27 S·cm2·mol–1 Λ = 421,27 – (60,65 + 0,230 · 421,27) Konduktivita na začátku měření: κ = Λ · c · 10–3 = 410,13(S·cm2·mol-1) · Konduktivita roztoku v bodě ekvivalence (v roztoku je NaNO3): Λo = λo(Na+) + λo(NO3-) = 50,1 + 71,46 = 121,56 S·cm2·mol–1 Λ = 121,56 – (60,65 + 0,230 · 121,56) κekv. = Λ · c · 10–3 = 115,29· Δκ = 2,051·10–3 – 5,76·10–4 = 1,475·10–3 S·cm–1 ≈ 1,5·10–3 S·cm–1 Změna konduktivit během titrace: b) Výše uvedená rovnice je omezena na nižší koncentrace. S vědomím určité nepřesnosti použijeme hodnoty z části a). Měrná vodivost v bodě ekvivalence se bude rovnat počáteční vodivosti (0,02 S cm–1) zmenšené o specifickou vodivost HNO3 a zvětšené o konduktivitu NaNO3: κ = 0,02 – 2,051·10–3 + 5,76·10–4 = 0,0185 S·cm–1 Δκ = 0,02 – 0,0185 = 1,50·10–3 S·cm–1 Relativní změna specifické vodivosti: | ||
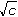 ,
,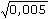 = 410,13 S·cm2·mol–1
= 410,13 S·cm2·mol–1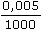 (mol·cm-3) = 2,051·10–3 S·cm–1
(mol·cm-3) = 2,051·10–3 S·cm–1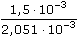 ·100 =
·100 =  změna konduktivity v roztoku s neutrální solí je stejná
změna konduktivity v roztoku s neutrální solí je stejná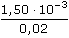 ·100 =
·100 =