|
- Příklad 6.26




- Objem 100 ml 0,01 molárního roztoku kovového iontu byl titrován roztokem ligandu téže
koncentrace. Kovový ion a ligand tvoří komplex 1:1 (ML). Vypočtěte pM po přídavku 0%, 90, 99,9%, 100%, 100,1% 110% a 150% titrantu,
je-li βML: a) 108, b) 1012, c) 1020
Řešení a) Objem 100 ml 0,01 molárního roztoku kovového iontu Mz+ je titrován roztokem ligandu Lm- téže koncentrace. βML = 1081) Přídavek titrantu 0 %:pM = –log [Mz+] = –log 0,01 = 2,00 2) Přídavek titrantu 90 %, tj. 90 ml[Mz+] = 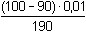 = 5,26·10–4 mol·l–1 pM = 3,28 = 5,26·10–4 mol·l–1 pM = 3,28 3) Přídavek titrantu 99,9 %,tj. 99,9 ml[Mz+]r = 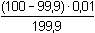 = 5,00·10–6 mol·l–1 = 5,00·10–6 mol·l–1Konstanta stability βMY je nízká, produkt disociace vzniklého komplexu bude významně zvyšovat koncentraci volného kationtu. Kořen kvadratické rovnice (7), resp. (20a) představuje koncentrační navýšení Mz+:[Mz+]dis2 + βML-1·[Mz+]dis – βML-1·cM = 0[M z+] dis2 + 10 -8·[M z+] dis - 10 -8·0,005 = 0  [M z+] dis = 7,066·10 -6 mol·l –1pM = 4,92 4) Přídavek titrantu 100 %, tj. 100 mlV roztoku je pouze částečně disociovaný komplex ML. Protože [Mz+]dis = [Ln-], lze k řešení použít substitucí [L] upravený vztah (5) a další úpravou se obdrží rovnice (7), resp. (20a).[Mz+]dis2 + βML-1·[Mz+]dis – βML-1·cM = 0[M z+] dis2 + 10 -8·[M z+] dis - 10 -8·0,005 = 0  [M z+] dis ≈ 7,07·10 -6 mol·l –1 K témuž výsledku lze dospět i podle (20): pM = 1/2(log βML – log cM) = 1/2(8 – log 0,005) = 5,15 5) Přídavek titrantu 100,1 %, tj. 100,1 ml:Konstanta stability βML je nízká, disociace vzniklého komplexu bude zvyšovat koncentraci nadbytečného ligandu. Koncentrační navýšení [Lm–]dis představuje: kořen kvadratické rovnice (7), resp. (20a)[Lm-]dis2 + βML-1·[Lm-]dis – βML-1·cM = 0[L m-] dis2 + 10 -8·[L m-] dis - 10 -8·0,005 = 0  [L m-] dis = 7,066·10 -6 mol·l –1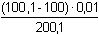 = 5,00·10–6 mol·l–1 = 5,00·10–6 mol·l–1[Lm-] = [Lm-]r + [Lm-]dis = 5,00·10–6 + 7,066·10–6 ≈ 1,21·10–5 mol·l–1 Koncentrace [Mz+] se zjistí ze vztahu (5), resp. (21):[Mz+] = 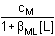 = = 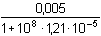 = 4,13·10–6 mol·l–1 = 4,13·10–6 mol·l–1  pM = 5,38 pM = 5,38 6) Přídavek titrantu 110 %, tj. 110 ml:Rovnovážná koncentrace ligandu: [Lm-] = cL – cM = 4,76·10–4 mol·l–1[Mz+] = 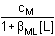 = = 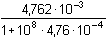 = 1,00·10–7 mol·l–1 = 1,00·10–7 mol·l–1  pM = 7,00 pM = 7,00 7) Přídavek titrantu 150 %, tj. 150 ml:Rovnovážná koncentrace ligandu: [Lm-] = cL – cM = 0,002 mol·l–1[Mz+] = 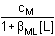 = = 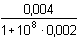 = 2,00·10–8 mol·l–1 = 2,00·10–8 mol·l–1  pM = 7,70 pM = 7,70 Postup řešení příkladů b), c) s vyššími konstantami stability chelátů je zcela analogický. Příspěvek disociace na obsah složek je v těchto případech zanedbatelný.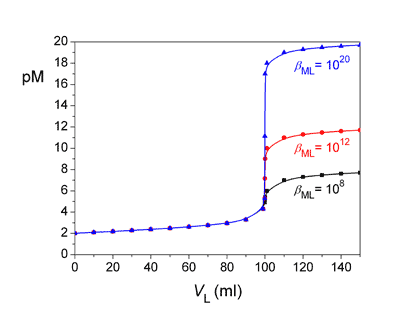
Titrační křivka pro titraci 100 ml roztoku kovového iontu Mn+ (c = 0,01 mol·l-1) odměrným roztokem ligandu (c = 0,01 mol·l-1) a pro různé konstanty stability komplexu βML. Zpět
|
|




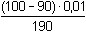 = 5,26·10–4 mol·l–1 pM = 3,28
= 5,26·10–4 mol·l–1 pM = 3,28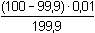 = 5,00·10–6 mol·l–1
= 5,00·10–6 mol·l–1 [Mz+]dis = 7,066·10-6 mol·l–1
[Mz+]dis = 7,066·10-6 mol·l–1 [Mz+]dis ≈ 7,07·10-6 mol·l–1
[Mz+]dis ≈ 7,07·10-6 mol·l–1 [Lm-]dis = 7,066·10-6 mol·l–1
[Lm-]dis = 7,066·10-6 mol·l–1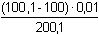 = 5,00·10–6 mol·l–1
= 5,00·10–6 mol·l–1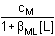 =
= 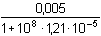 = 4,13·10–6 mol·l–1
= 4,13·10–6 mol·l–1  pM = 5,38
pM = 5,38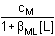 =
= 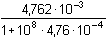 = 1,00·10–7 mol·l–1
= 1,00·10–7 mol·l–1  pM = 7,00
pM = 7,00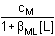 =
= 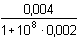 = 2,00·10–8 mol·l–1
= 2,00·10–8 mol·l–1  pM = 7,70
pM = 7,70