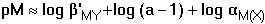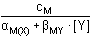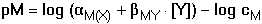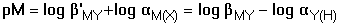| |||||
|
Chelatometrické titrační křivky představují závislost rovnovážné koncentrace kovového iontu M na množství odměrného roztoku titrantu T (chelatonu Y), obvykle udávanou (vzhledem k nízké rovnovážné koncentraci kovu) ve tvaru pM = f(cY), resp. pM = f(a), kde a = cY/cM. V celém průběhu křivky platí soustava rovnic
cM = [M'] + [MY]
cY = [Y'] + [MY]
Jednotlivé body titrační křivky lze určit z následujících vztahů: a) a = 0 cM = [M'] = [M]αM(X) b) a < 1 [M'] = cM - cY = (1 - α)cM a = 0,5 [M'] = [MY] = cM/2 = [M]αM(X) c) a = 1 [M'] = [Y'] a [MY] = cM β'MY = cM/[M']2 =
cM/([M]αM(X))2
resp. pM = Je-li komplex málo stabilní (β'MY < 108), je třeba uvažovat disociaci, neboť [MY] ≠ cM:
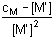
 βMY = βMY =
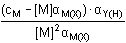
Koncentrace [M] pak představuje kladný kořen kvadratické rovnice. d) a > 1 [M'] = resp. [M] = a = 2 [MY] = [Y']
Řešené příklady:
| ||
| |||||

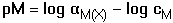
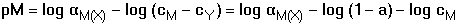
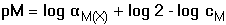
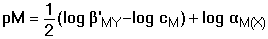
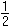 (log βMY - log cM
+ log αM(X) - log αY(H))
(log βMY - log cM
+ log αM(X) - log αY(H))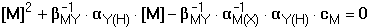
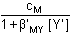 [Y'] = cY - cM = (a - 1)cM
[Y'] = cY - cM = (a - 1)cM