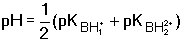| |||||
|
Neúplnou neutralizací vícesytných kyselin nebo zásad vznikají hydrogensoli - amfolyty, které se podle podmínek chovají buď jako kyseliny nebo zásady. Např. amfolyt od dvojsytné kyseliny HA– HA- + H2O
H2O + H2A
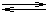 A2– + H3O+ ........ K2
A2– + H3O+ ........ K2 H3O+ + HA-
........ K1 H3O+ + HA-
........ K1
Rovnováhám přísluší disociační konstanty K1 a K2. Vztahy pro výpočet koncentrace hydroxoniových iontů, resp. pH, odvodíme na základě vzájemné kombinace tří faktorů: látkové bilance kyseliny (68), podmínky elektroneutrality roztoku (69) a disociačních konstant. Protože amfolyt je silný elektrolyt, platí: c(HA-) = [M+] = c(H2A), kde M+ je protiion k aniontovému amfolytu. Dosazením rovnice (68) do (69) za [M+] a úpravou s využitím příslušných rovnovážných konstant se získá rovnice (70):
Za [HA-] se obvykle dosazuje celková koncentrace hydrogensoli c(MHA). Vypočtená hodnota [H3O+] je dostatečně správná, pokud platí Koncentrace [H2A] a [A2-] se vypočítají ze vztahů pro K1 a K2, do nichž se dosadí [H3O+] z rovnice (70). Není-li podmínka (71) splněna, dosadí se vypočítané koncentrace [H2A] a [A2-] do vztahu (68) a vypočítá se správnější hodnota [HA-] {tzn. [HA-] ≠ c(MHA)}. Ze vztahu (70) se pak zjistí nová hodnota [H3O+]. V aproximaci se pokračuje tak dlouho, až dvě po sobě získané hodnoty pH se liší o méně než 0,02 jednotky. Zpravidla však bývá, že součin (K2 · [HA–]) » Kw, takže vztah lze zjednodušit na tvar v němž lze obvykle rovnovážnou koncentraci amfolytu nahradit celkovou analytickou koncentrací,
tj. Je-li také [HA-] » K1, je konstanta ve jmenovateli zanedbatelná vůči [HA-] a dospějeme k dalšímu zjednodušení: Obecně pro i-tý amfolyt lze použít následující tvar rovnic: Obdobné vztahy lze odvodit pro amfolyty vícesytných zásad:Řešený příklad:
| ||
| |||||

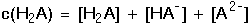
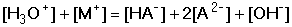
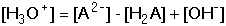
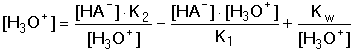
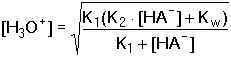
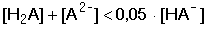
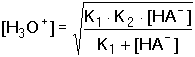
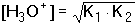
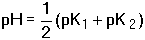 (73)
(73)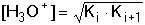
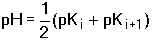 (73a)
(73a)