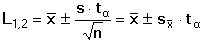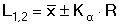| |||||
|
Náhodné chyby vznikají při každém měření a tedy ovlivňují přesnost výsledků. Jsou způsobeny drobnými nepřesnostmi při vážení nebo měření, nedokonalostí odečítání sledované veličiny atp. Mají nepravidelný charakter s tendencí vzájemné kompenzace, jsou zpravidla malé a jejich přesná příčina není známá. Rozdělení náhodných chyb, tj, závislost pravděpodobnosti výskytu chyb na jejich
absolutní velikosti |xi – μ|, charakterizuje v grafickém vyjádření Gaussova křivka,
která má dva parametry. Parametr μ určuje polohu maxima křivky vzhledem k vodorovné ose a
parametr σ vystihuje šířku křivky, tj. rozptýlení. Čím je rozptyl menší, tím je křivka užší,
symetričtější s velkou četností správných dat, tj. s nulovou chybou - hodnocený soubor je
přesnější. Nejlepším odhadem parametru μ je aritmetický průměr
Rozdíl naměřené hodnoty od průměru (xi – užívaným také v kalkulačkách se zabudovaným statistickým programem. Při malém počtu paralelních stanovení (n << 10) lze směrodatnou odchylku odhadnout z rozpětí R (viz kap. 4.1.): kde kn je Dean-Dixonův koeficient (tab. 3). Výpočet sR je značně jednoduchý a lze jej tedy využít k hodnocení m sérií při stejném počtu n paralelních měření v každé sérii. Potřebné průměrné rozpětí se vypočítá podle vztahu Relativní mírou přesnosti série paralelních stanovení je tzv. relativní směrodatná odchylka sr (dříve užívaný variační koeficient se nedoporučuje), většinou uváděná v procentech: Směrodatná odchylka a stejně i relativní směrodatná odchylka budou tím menší, čím přesnější budou výsledky měření. Pro danou analytickou metodu je tedy určitou veličinou, která charakterizuje reprodukovatelnost daného počtu paralelních měření. Mírou přesnosti aritmetického průměru je směrodatná odchylka průměru
Ze vztahů vyplývá, že s nárůstem počtu měření se zvyšuje přesnost stanovení (hodnota
U většiny hodnocených sérií měření (stanovení) neznáme skutečnou hodnotu μ. Na základě matematické statistiky však lze vymezit oblast, v níž se s určitou pravděpodobností (na předem zvolené hladině významnosti) skutečná hodnota nachází. Tato oblast - interval spolehlivosti L1,2 - je tím užší, čím jsou získané výsledky přesnější, charakterizuje spolehlivost výsledku. Prvý způsob výpočtu intervalu využívá Studentova rozdělení kde L1 a L2 označují krajní meze intervalu spolehlivosti, tα je kritická hodnota Studentova rozdělení pro zvolenou hladinu významnosti α (tab. 4). Druhý způsob, navržený Dean-Dixonem pro malé soubory, využívá Lordovo rozdělení kde Kα je kritická hodnota Lordova rozdělení pro zvolenou hladinu významnosti α (tab. 4). Řešené příklady:
| ||
| |||||

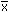 , parametru σ je
směrodatná (standardní) odchylka s, která je mírou přesnosti série paralelních
výsledků.
, parametru σ je
směrodatná (standardní) odchylka s, která je mírou přesnosti série paralelních
výsledků.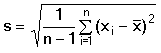

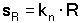
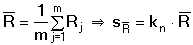
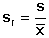
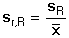
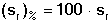 (9)
(9)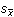
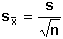
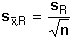 (10)
(10)