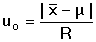|
4.3. Soustavné chyby
4.3.1. Testování správnosti výsledků
Aritmetický průměr výsledků série stanovení (měření) je správný, pokud jeho
rozdíl od skutečné hodnoty 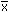 - μ s určitou
pravděpodobností (na zvolené hladině významnosti α) není statisticky významný.
Skutečnou hodnotu μ obvykle neznáme a tedy ji nahrazujeme konvenčně správnou hodnotou
(tzv. "analytické standardy", "normály" nebo "etalonové referenční materiály") nebo analýzou
vzorku se známými přídavky stanovované složky. - μ s určitou
pravděpodobností (na zvolené hladině významnosti α) není statisticky významný.
Skutečnou hodnotu μ obvykle neznáme a tedy ji nahrazujeme konvenčně správnou hodnotou
(tzv. "analytické standardy", "normály" nebo "etalonové referenční materiály") nebo analýzou
vzorku se známými přídavky stanovované složky.
K testování používáme buď směrodatnou odchylku - Studentův t-test správnosti
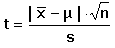 = =
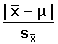 (13) (13)
nebo rozpětí R pro malý počet výsledků (n < 10) - Lordův uo - test správnosti
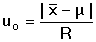 (14) (14)
Vypočtenou hodnotu t nebo uo srovnáváme s kritickou hodnotou tα nebo
Kα (tab. 4) pro
daný počet stanovení. Je-li t < tα nebo uo < Kα,
rozdíl |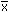 - μ| je s určitou
pravděpodobností způsoben pouze náhodnými chybami a zjištěný výsledek je správný. V opačném
případě je výsledek zatížen soustavnou chybou. - μ| je s určitou
pravděpodobností způsoben pouze náhodnými chybami a zjištěný výsledek je správný. V opačném
případě je výsledek zatížen soustavnou chybou.
Řešené příklady:
- Příklad 4.4

- Polarografické stanovení zinku z příkladu 4.2. otestujte
na hladině významnosti α = 0,05 vzhledem ke standardní metodě (atomové absorpční
spektrometrii - AAS), podle níž je 144,20 μg zinku v 1 litru vody!
- Příklad 4.5

- Elementární analýzou organické látky byl zjištěn následující obsah uhlíku:
48,05 %, 48,15 %, 48,08 %, 47,80 %, 48,12 %. Vypočítaný obsah uhlíku ze vzorce
organické látky je 48,19 %. Otestujte správnost výsledků pro α = 0,05 a 0,01 !
|
|

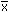 - μ s určitou
pravděpodobností (na zvolené hladině významnosti α) není statisticky významný.
Skutečnou hodnotu μ obvykle neznáme a tedy ji nahrazujeme konvenčně správnou hodnotou
(tzv. "analytické standardy", "normály" nebo "etalonové referenční materiály") nebo analýzou
vzorku se známými přídavky stanovované složky.
- μ s určitou
pravděpodobností (na zvolené hladině významnosti α) není statisticky významný.
Skutečnou hodnotu μ obvykle neznáme a tedy ji nahrazujeme konvenčně správnou hodnotou
(tzv. "analytické standardy", "normály" nebo "etalonové referenční materiály") nebo analýzou
vzorku se známými přídavky stanovované složky.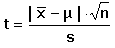
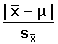 (13)
(13)