|
- Příklad 4.19




- Měď v rudě byla stanovena chelatometricky a jodometricky s výsledky:
chelatometrie: 40,2 40,8 41,2 40,4 41,0 40,1 % Cu
jodometrie: 42,01 41,55 40,98 42,08 41,85 41,00 % Cu
Standardní metodou (elektroanalýzou) byl stanoven obsah 40,85 % Cu. Zjistěte, zda
rozdíl průměrů výsledků dvou postupů je významný pro α = 0,05; jestliže ano, pak
která z metod je zatížena soustavnou chybou!
Řešení | Chelatometrie (A) | Jodometrie (B) | Výsledky (% Cu):
40,1
40,2
40,4
40,8
41,0
41,2
Průměr: = 40,617 | Výsledky (% Cu):
40,98
41,00
41,55
41,85
42,01
42,08
Průměr: = 41,578 | | sA (% Cu): 0,4491 | sB (% Cu): 0,4909 | | Rozptyl: (sA)2 = 0,2017 | Rozptyl: (sB)2 = 0,2410 | | Rozpětí: RA = 1,10 [%] | Rozpětí: RB = 1,10 [%] |
Počet paralelních stanovení v obou souborech je stejný: n = 6.Směrodatné odchylky byly zjištěny pomocí vztahu (6). Test sourodosti podle vztahu (15): FB = 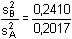 = 1,1948 < Fα=0,05 = 5,050 = 1,1948 < Fα=0,05 = 5,050 Poměr rozptylů není statisticky významný, výsledky jsou sourodé. Lze tedy provádět test shodnosti průměrů dvou souborů.Test shodnosti dvou průměrů: a) podle vztahu (16), b) podle vztahu (17): a) t = 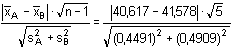 = 3,2301 > t11 = 2,228 = 3,2301 > t11 = 2,228b) u = 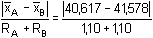 = 0,4368 > uα=0,05 = 0,250 = 0,4368 > uα=0,05 = 0,250 Oběma postupy je prokázáno, že rozdíl průměrů nezávislých stanovení je statisticky významný. Soubory nejsou shodné. Test správnosti výsledků (soustavné chyby): a) podle vztahu (13), b) podle vztahu (14): Soubor A:a) t = 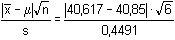 = 1,271 < tα=0,05 = 2,571 = 1,271 < tα=0,05 = 2,571b) u = 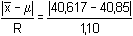 = 0,212 < Kα=0,05 = 0,399 = 0,212 < Kα=0,05 = 0,399 Soubor B:a) t = 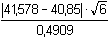 = 3,633 > tα=0,05 = 2,571 = 3,633 > tα=0,05 = 2,571b) u = 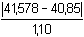 = 0,662 > Kα=0,05 = 0,399 = 0,662 > Kα=0,05 = 0,399 Soubor B (jodometrie) je zatížený soustavnou chybou, neboť rozdíl |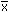 - μ| je statisticky významný. - μ| je statisticky významný. Zpět
|
|




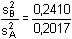 = 1,1948 < Fα=0,05 = 5,050
= 1,1948 < Fα=0,05 = 5,050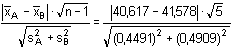 = 3,2301 > t11 = 2,228
= 3,2301 > t11 = 2,228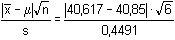 = 1,271 < tα=0,05 = 2,571
= 1,271 < tα=0,05 = 2,571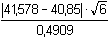 = 3,633 > tα=0,05 = 2,571
= 3,633 > tα=0,05 = 2,571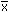 - μ| je statisticky významný.
- μ| je statisticky významný.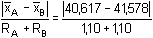 = 0,4368 > uα=0,05 = 0,250
= 0,4368 > uα=0,05 = 0,250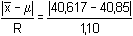 = 0,212 < Kα=0,05 = 0,399
= 0,212 < Kα=0,05 = 0,399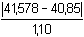 = 0,662 > Kα=0,05 = 0,399
= 0,662 > Kα=0,05 = 0,399