|
- Příklad 5.175




- Objem 10 ml 0,1 molárního diethylaminu byl titrován roztokem kyseliny chlorovodíkové
koncentrace 0,1 mol·l-1. Jaké pH bude mít roztok vytitrovaný na 0%, 10%, 50%,
99% a 100%?
Řešení Disociační konstanty diethylamonia a diethylaminu:pKBH+ = 10,98 KBH+ = 1,047·10–11;pKB = 3,02 KB = 9,55·10–4 a) pH 0,1M-(C2H5)2NH podle vztahu (36):pH = pKw – 1/2(pKB – log cB) = 14 – 1/2(3,02 – log 0,1) = 14 – 2,01 = 11,99 Protože pOH = 2,02 < 1,30 – log 0,1, je třeba upřesnit výpočet podle rovnice (37b):[OH–]2 + KB·[OH–] – KB·cB = 0[OH–]2 + 9,55·10–4·[OH–] – 9,55·10–5 = 0 [OH–] = 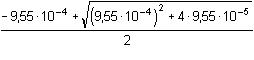 = 9,306·10–3 mol·l–1 = 9,306·10–3 mol·l–1pOH = 2,03  pH = 11,97 b) Vytitrováno 10% analytu – roztok obsahuje dvě složky: BH+ a BProtože koncentrace analytu a HCl jsou stejné, objem se zvětšil o 1/10, tj. o 0,1 ml [BH+] = [HCl] = 1·0,1 / 11 = 9,091·10–3 mmol·ml–1 = mol·l–1[B] = cB – [BH+] = (10-1)·0,1 / 11 = 0,08182 mmol·ml–1 = mol·l–1 Podle vztahu (79)pH = pKw – pOH = 14 – (3,02 + log 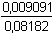 ) = 14 – 2,07 = 11,93 ) = 14 – 2,07 = 11,93 Protože pKB < 7 a 1,30 – log c BH+ > pOH < 1,30 – log c B, je možné upřesnit hodnotu pOH podle vztahu (77), převedeného do tvaru kvadratické rovnice: [OH–]2 + (cBH+ + KB)·[OH–] – KB·cB = 0[OH–]2 + (0,009091 + 9,55·10–4)·[OH–] – 9,55·10–4 · 0,08182 = 0 [OH–] = 5,144·10–3 mol·l–1 pOH = 2,29  pH = 11,71 pH = 11,71 c) Vytitrováno 50% analytu – roztok obsahuje dvě rovnovážné složky BH+ a B v poměru koncentrací 1:1,
tzn. [BH+] = [B]Ze vztahu (79) vyplývá, že pH = pK BH+ = 10,98d) Vytitrováno 99% analytu – objem se zvětšil o 9,9 ml [BH+] = 9,9·0,1 / 19,9 = 0,0497 mmol·ml–1 = mol·l–1[B] = (10 – 9,9)·0,1 / 19,9 = 5,025·10–4 mmol·ml–1 = mol·l–1 Podle (79): pH = 10,98 – log 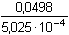 = 10,98 – 1,996 ≈ 8,98 = 10,98 – 1,996 ≈ 8,98e) Vytitrováno 100% titrantu – v roztoku je pouze kation slabé zásady BH+ [BH+] = cBH+ = 10·0,1 / 20 = 0,05 mmol·ml–1 = mol·l–1 Podle vztahu (61): pH = 1/2(pKBH+ – log cBH+) = 1/2(10,98 – log 0,05) = 6,14Zpět
|
|




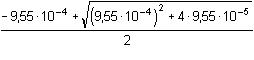 = 9,306·10–3 mol·l–1
= 9,306·10–3 mol·l–1 pH = 11,97
pH = 11,97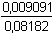 ) = 14 – 2,07 = 11,93
) = 14 – 2,07 = 11,93 pH = 11,71
pH = 11,71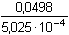 = 10,98 – 1,996 ≈ 8,98
= 10,98 – 1,996 ≈ 8,98