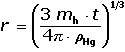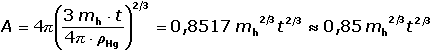| |||||
|
Polarografie je elektrolytická metoda, při níž se sleduje závislost proudu na lineárně rostoucím stejnosměrném napětí, vkládaném na dvojici elektrod ponořených do zkoumaného roztoku. Pracovní elektrodou je rtuťová kapající elektroda. Použije-li se jako pracovní elektroda rtuťová s konstantním povrchem (statická, visící, filmová), uhlíková (pastová, kompozitní, skelný uhlík aj.) či kovová (platinová, zlatá), mluvíme o voltametrii. VII.1. Rtuťová kapající (kapková) elektroda (DME)Funkci elektrody charakterizují tzv. konstanty kapiláry – průtoková rychlost rtuti mh a doba kapky t. V řadě případů je doplňuje povrch rtuťové kapky A. Průtoková rychlost mh – hmotnost rtuti, která vyteče z kapiláry za 1 vteřinu, se řídí Hagen–Poiseuillovým zákonem: kde rk – vnitřní poloměr kapiláry, d – délka kapiláry, ρHg – hustota rtuti (13,53 g·cm–3), η – viskozita rtuti [Pa·s], pe – efektivní hydrostatický tlak: kde g – tíhové zrychlení (9,81 m·s–2), hm – výška sloupce rtuti (od ústí kapiláry po hladinu rtuti), hz – výška sloupce rtuti odpovídající zpětnému tlaku, který působí proti růstu kapky (důsledek mezipovrchového napětí rtuť/ roztok, u běžných kapilár hz ~ 2 cm) Doba kapky t - závisí na tíze rtuti. Kapka odkápne, když její tíha G překoná povrchové síly, které ji drží při ústí kapiláry: G = mh · t · g = 2 π · rk · γ kde γ – povrchové napětí rtuti, základní rozměr: [N·m-1] Povrch rtuťové kapající elektrody A - se mění s časem. Pro kulový tvar platí: A = 4π·r2 Z objemu kapky V = a následně okamžitý povrch A v čase t: Číselný faktor v rovnici (VII.5) má rozměr: cm2·g–2/3. Dosadí-li se mh v g·s-1 a t (resp. τ) v sekundách, plocha A vyjde v cm2.
Příklady
| ||
| |||||

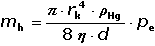
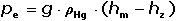
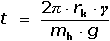
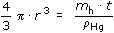 lze
vypočítat její poloměr r
lze
vypočítat její poloměr r