



ŘešeníEoCu2+/Cu = 0,337 V (tab.1) a) Měď lze vylučovat až do potenciálu –0,43 V, jemuž odpovídá koncentrace (podle rovnice IV.2): ECu = EoCu2+/Cu + 0,0296 log [Cu2+] ..... při 25 °C –0,43 = 0,337 + 0,0296 log [Cu2+] Po elektrolýze při potenciálu –0,43 V zůstává v roztoku: log [Cu2+] = –0,767 / 0,0296 = –25,91 Vyloučení Cu vedle Cd v nepřítomnosti KCN je kvantitativní. b) Protože potenciál měděné elektrody je v 0,4M-KCN zápornější (ECu = –0,97 V; ECd = –0,892 V ), c) Potenciál katody je určován aktivitou komplexně vázaného iontu: β4 = Ek = EoCd2+/Cd – 0,0296 (log β4 + 4 log [CN–]) + 0,0296 log [Cd(CN)42–] Ek = Eok + 0,0296 log [Cd(CN)42–] = –0,862 + 0,0296 log [Cd(CN)42–] Lze předpokládat, že v prostředí s nadbytkem KCN je koncentrace komplexního iontu rovna původní koncentraci Cd2+–iontu; z podmínek zadání tedy plyne: –0,892 = Eok + 0,0296 log 0,1 |·(–1) –0,980 = Eok + 0,0296 log [Cd(CN)42–] (–0,980 + 0,892) = 0,0296 + 0,0296 log [Cd(CN)42–] log [Cd(CN)42–] = (–0,088 – 0,0296) / 0,0296 = –3,9730 [Cd(CN)42–] = 1,06·10-4 mol·l-1 nebo –0,892 = Eok – 0,0296 –0,980 = –0,862 + 0,0296 log [Cd(CN)42–] | ||
 [Cu2+] =
[Cu2+] = 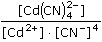 = 10-17,1
= 10-17,1