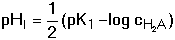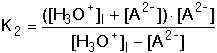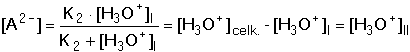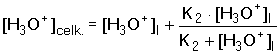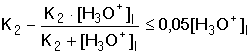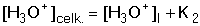5.3.4. Vícesytné slabé kyseliny a zásady

Disociační rovnováhy vícesytných kyselin a zásad jsou charakterizovány příslušnými konstantami K₁ až K_n. U analyticky významných protolytů je první konstanta mnohonásobně větší než následující, a tedy první disociační rovnováha bude mít rozhodující vliv na aciditu roztoku. V prvém kroku vypočítáme přibližnou hodnotu pH_I dvojsytné kyseliny podle již známého vztahu

   (45)

kterou zpřesňujeme podle podmínek b) až d) v kap. 5.3.1.

Je-li pK2 > pH_I + 1,30 (tj. pK₂ > pH_I – log c_H2A), druhá disociační rovnováha je nevýznamná a hodnotu pH neovlivňuje.

Je-li však pK₂ < pH_I + 1,30, příp. je-li (pK₂ – pK₁) ≤ 1,5, je nezbytné hodnotu pH_I upřesnit přičtením koncentrace hydroxoniových iontů z disociace kyseliny do 2.stupně.

[H₃O⁺]_celk. = [H₃O⁺]_I + [H₃O⁺]_II

se obdrží kvadratická rovnice

[A^2-]² + (K₂ + [H₃O⁺]_I)[A^2-] – K₂·[H₃O⁺]_I = 0

Protože u slabé kyseliny je [A^2-] ≈ 0, lze kvadratický člen zanedbat

   (46)

    příp.     K₂ « [H₃O⁺]

   (47)

Zcela analogicky se postupuje při výpočtu koncentrace OH^–-iontů, resp. pOH, v roztocích vícesytných slabých zásad. V těchto případech ve vztazích figurují příslušné konstanty bazicity K_B.

Řešené příklady:

Příklad 5.76 

Vypočtěte pH roztoku 0,01 molární dvojsytné slabé kyseliny, jejíž disociační konstanty jsou pK₁ = 2,00 a pK₂ = 3,00 !

Příklad 5.77 

Vypočtěte pH 0,05 molárního roztoku kyseliny jantarové! pK₁ = 4,21, pK₂ = 5,64.

Příklad 5.78 

Vypočtěte pH roztoku 0,01 molárního roztoku šťavelanu sodného! Disociační konstanty kyseliny šťavelové jsou: pK₁ = 1,25, pK₂ = 4,285.